「同数発見」とは、たくさんの形や絵をすばやく数え、それらと同じ数の集まりを探す問題です。
ちなみに、異なる数を探すものは、「異数発見」です。
数に関する領域の中でも「同数発見」は、小学校受験でも度々出題されています。
同数発見の問題は、限られた時間の中でできるだけ速く正確にこなさなければならないため、それだけ難易度は高くなります。
ですから、まずはお子さんが、数をきちんと数えることが身についていることが必須となります。
数えとばしたり、数え間違えていたら、同じものを何度も数えなくてはならないからです。
まず、下の例題を見ていきましょう。
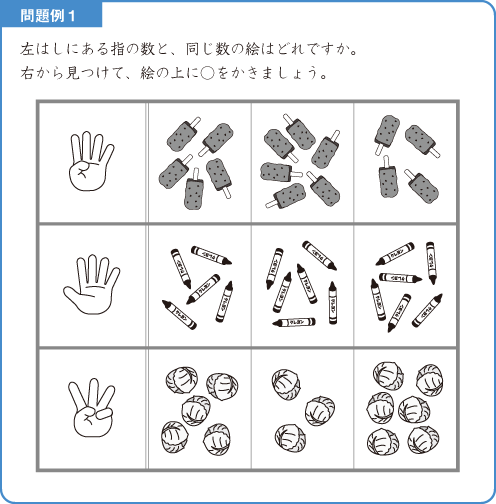
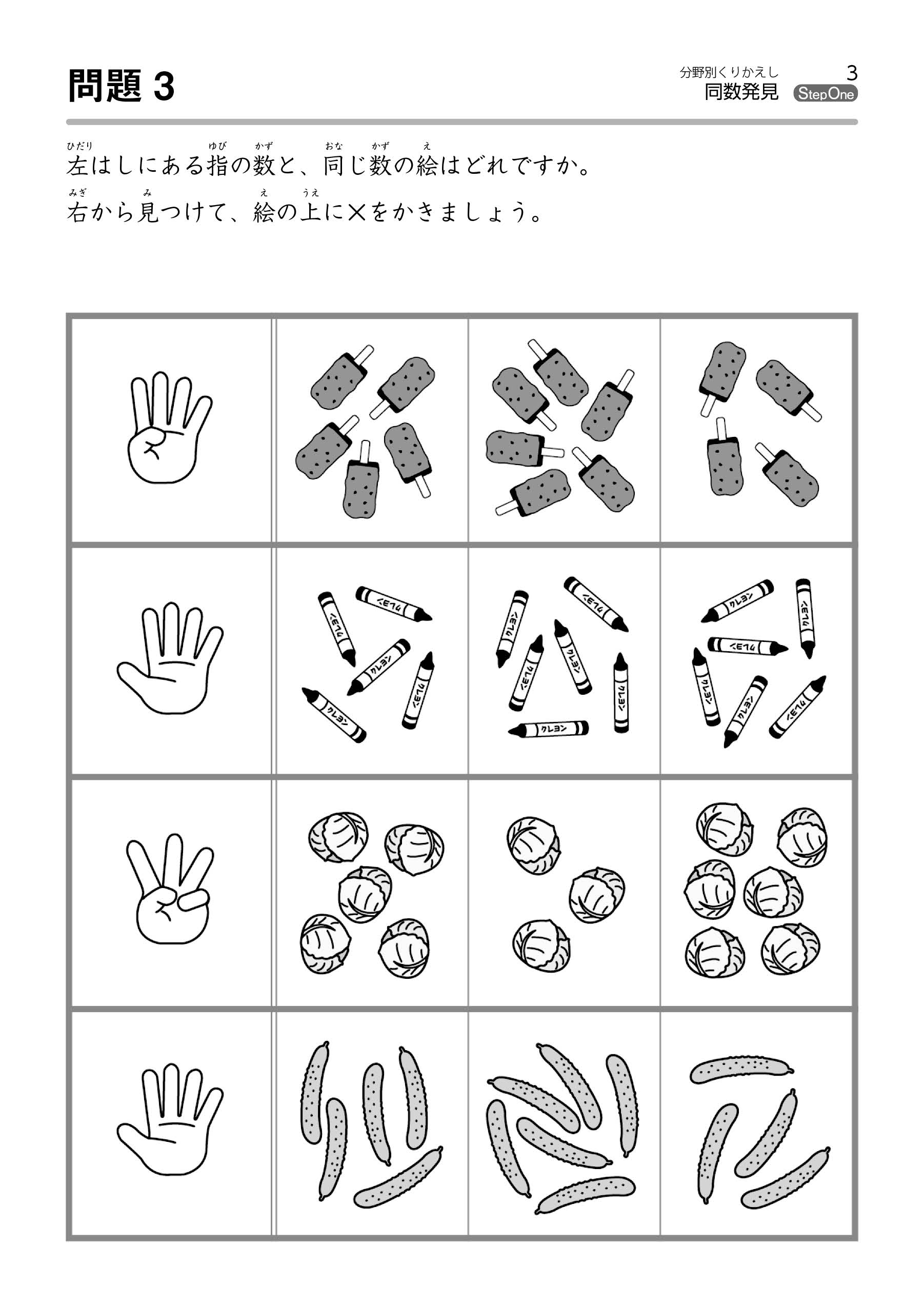
上記問題例1では、左側に指の絵があり、その指の数と同じ数のものを探しだす問題です。
指の数は「1、2、3、…」と数えなくても、絵を見てすぐに数が分かるのではないでしょうか。
指は普段から見慣れているからです。
同じように他のものであっても、少ない数であれば、そのかたまりをパッと見て、一つひとつ数えなくても数がわかるようになっていただきたいと思います。
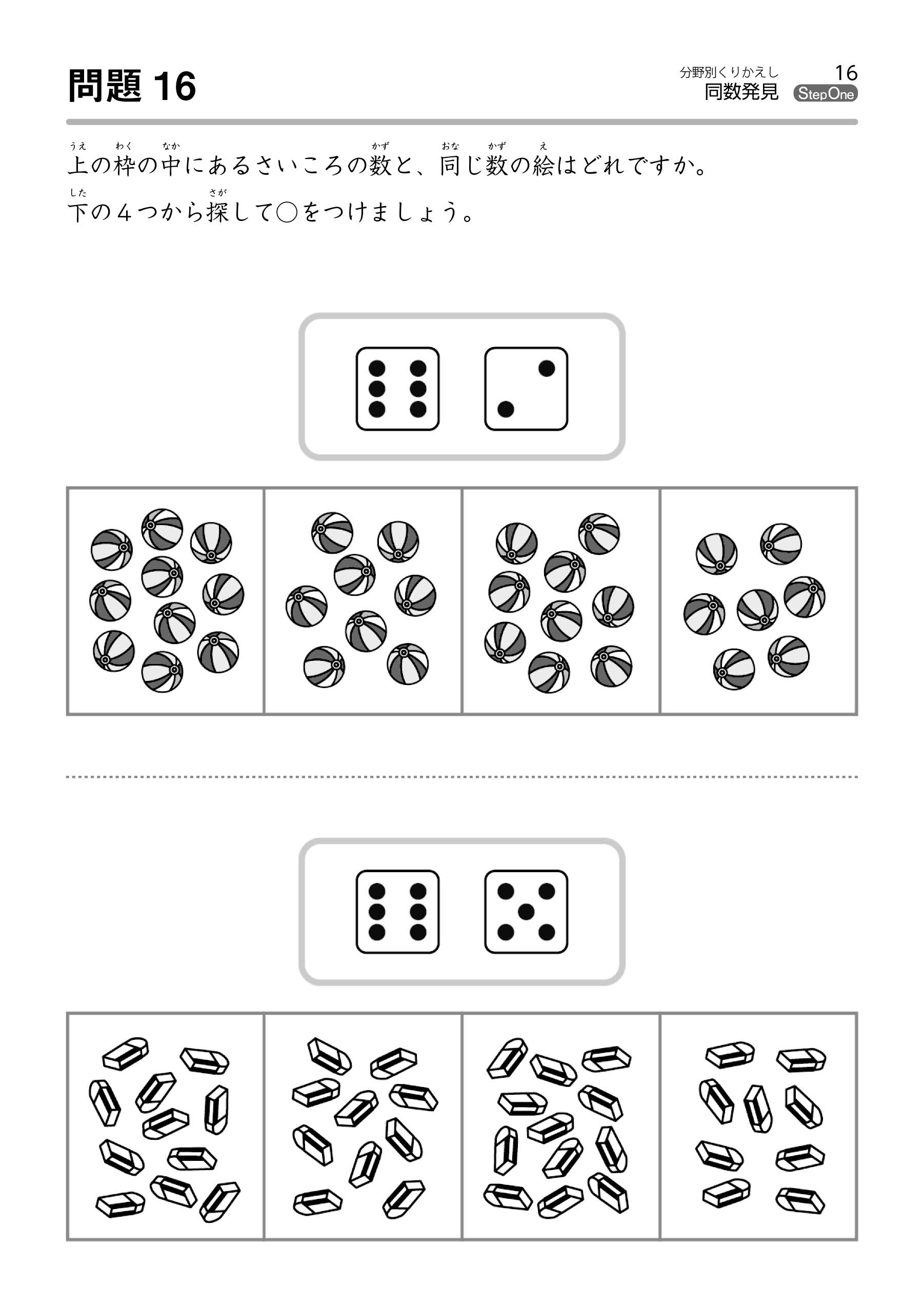
次の問題を見てみましょう。
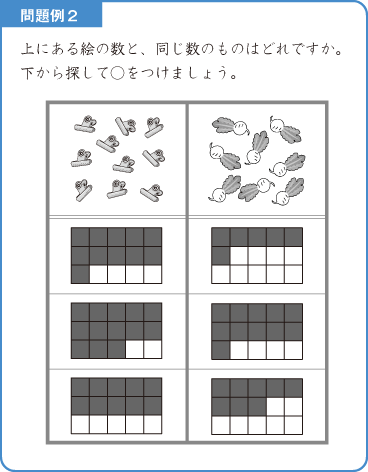
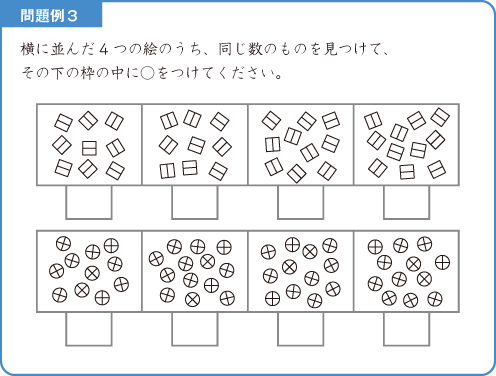
数が多くなってくると、数を素早く認識するのは難しいことです。
それでも、なるべく早く数えるために、「2、4、6、…」と、一度に2つずつ数える方法もあります(参考:下図1)。
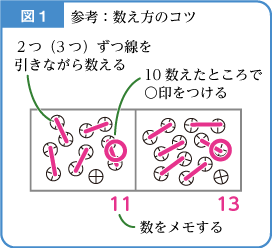
一つの枠の中の数を数えたら、前に数えた数を忘れてしまったということもよく聞きますが、最初のうちは、数えた数を数字でメモするのもいいでしょう。
ただ、自分が数えた数を覚えていくのも大切ですから、練習を繰り返すうちにメモなしでもできるようにしていただきたいと思います。
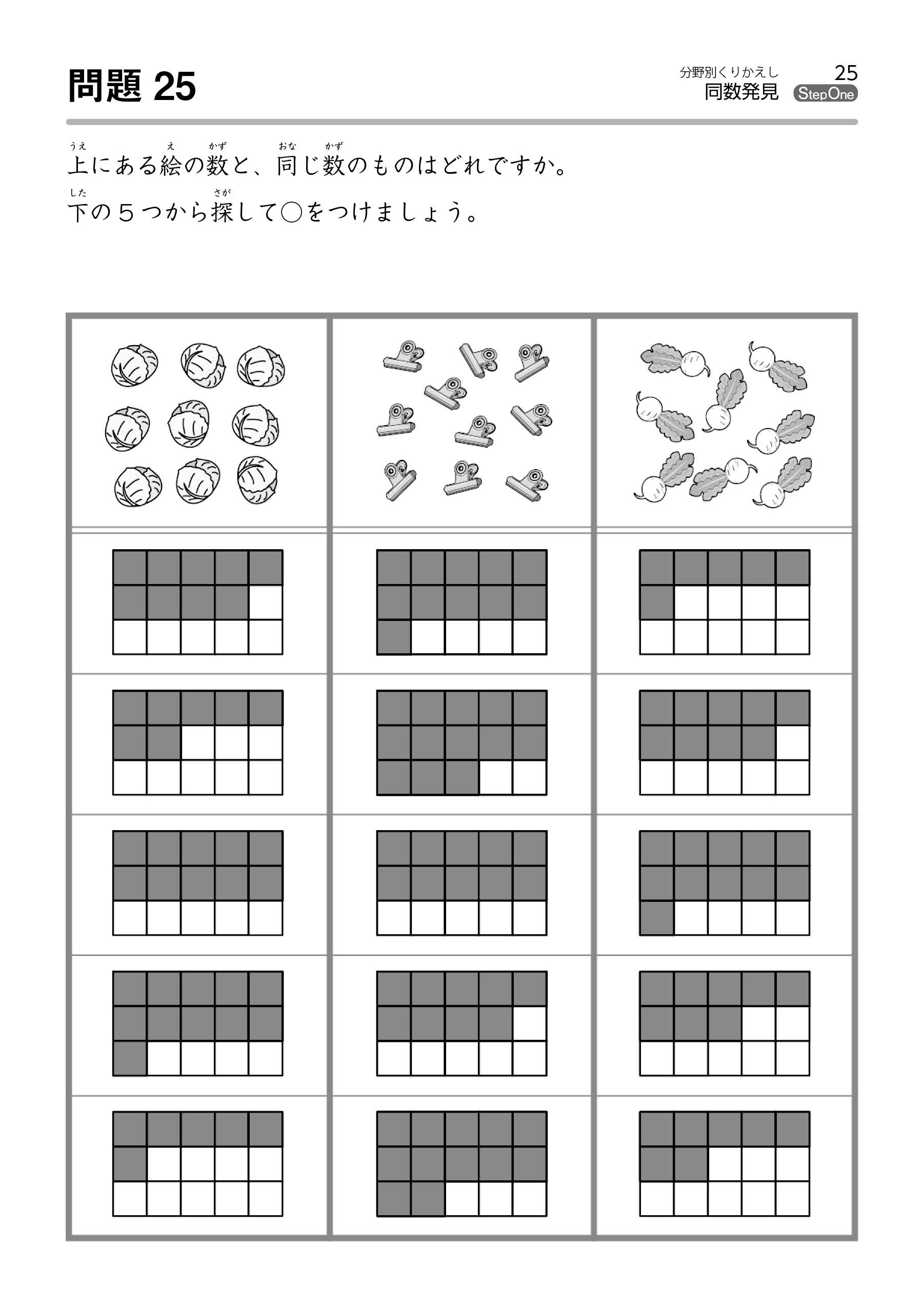
また、上記の問題例2のような問題では、解答欄のマス目は横が5つなので、「5、10、15、…」と5のかたまりで数えることができるとよいですね。
ご家庭でも日常生活の中の遊びの中に「数え方の工夫」を取り入れていただきたいと思います。
少ない数のまとまりであれば、数えなくてもパッと見てわかるように、また、数が多ければ「2ずつ」「5ずつ」あるいは「10ずつ」数えることができるようになれば、数の問題が好きになるし、自信がつき得意にもなっていくでしょう。
小学校受験では、難易度が高くなると、積み木を使った同数発見の問題も出されています。
お子さんの理解度を確かめながら、お子さんのペースに合わせて学習を進めていってください。
※異なる数を見つける「異数発見」教材もあわせてご利用ください。