さいころは小学校受験の算数の分野では定番となっている問題です。
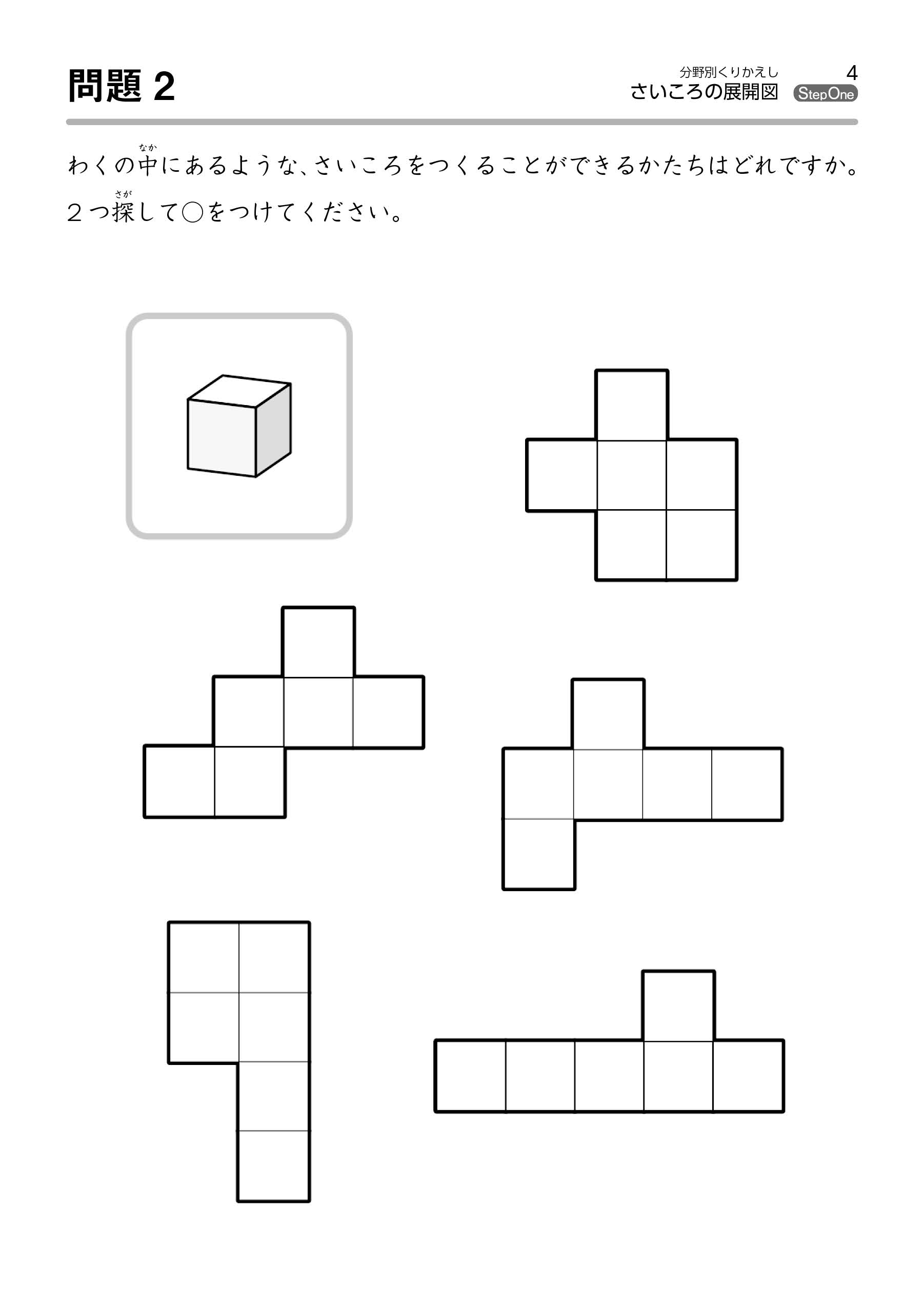
なかでも下記(問題例1)のような、展開図がいくつかあって、「組み立てたとき、さいころができるのはどれですか?」という問題をよく見かけます。
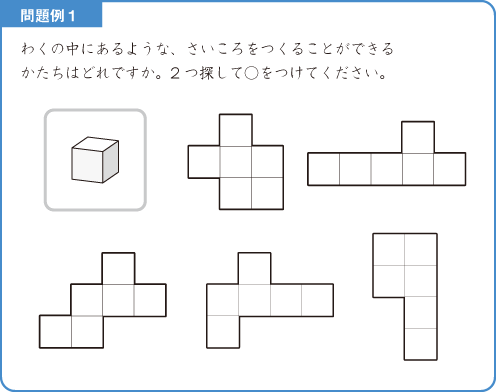
立方体の展開図は、回転させたものや、上下・左右に反転させて重なるものを1つとして数えると、全部で11種類あります(図1)。

小学校受験のテクニックとして、これらのかたちをすべて覚えるように指導するところもあります。
それも一つの方法ですが、この教材ではまず初歩の段階として、様々な展開図から立方体を作り上げる経験をさせてみることを基本としています。
未就学のお子さんには、実体験が大切です。
展開図を切り取って組み立て、実際にさいころ状になるか確かめてみましょう。
それでは、次の問題例2を見てみましょう。
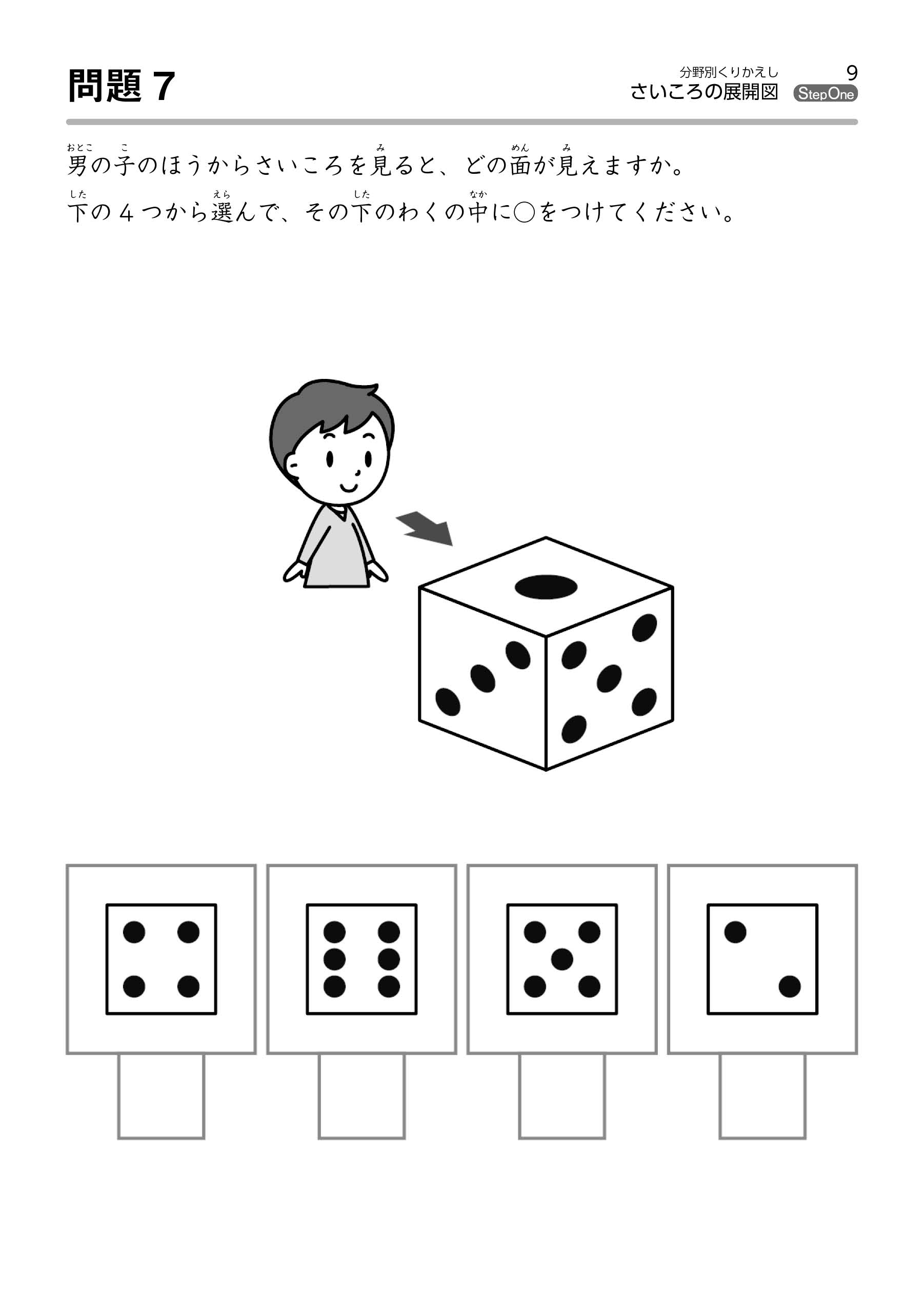
さいころを指定された方向から見て、その面の数字を答える問題です。
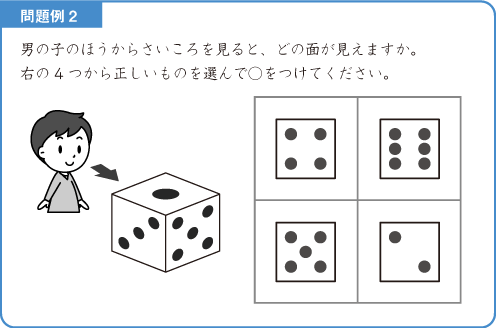
さいころは、向かい合う面の数を合わせると7になります。
これも実際にさいころを組み立てて観察してみましょう(図2)。
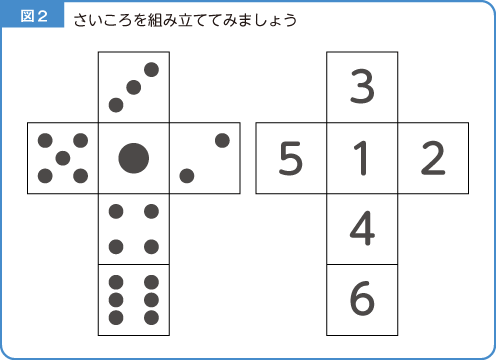
そのときに、
「さいころに使われている数字は何があるかな?(1~6の数字を答えさせる)」
「1の向かい側には6、2の向かい側には5、3の向かい側には4という数になっているね」
「合わせた数が必ず7になっているね」
「合わせたら7になる組み合わせは何と何があるかな」
「この面の裏側はどこの面になるかな」
などヒントを出してあげながら、お子さんが楽しくいろいろな発見ができるようにしてあげるといいですね。
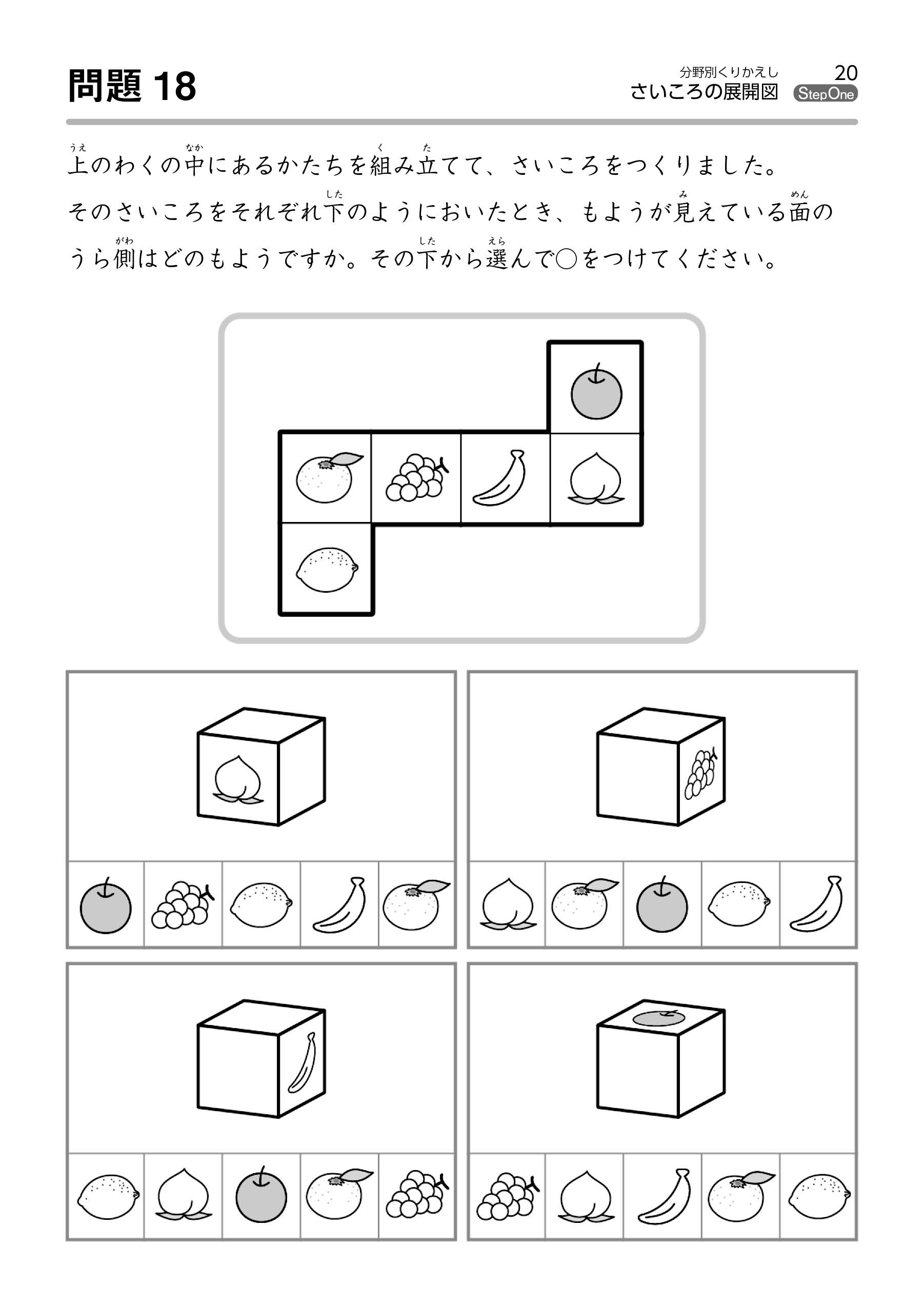
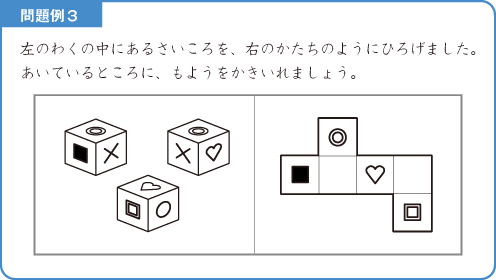
後半になってくると、難易度の高い発展問題も含まれています(問題例3・4)。
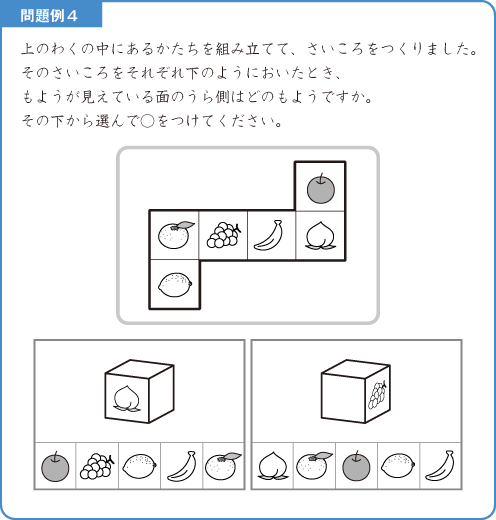
さいころの問題は、空間認識の問題です。
このような空間把握能力を問う問題は、様々な学習分野の中でも非常に難易度が高いです。
どの分野でも同じことが言えますが、やはりまずは実体験です。
ペーパーでの問題を解く前に、実際に紙を切って面を組み立て、立方体をつくってみてください。実体験を重ねていくことで、少しずつ空間認識ができるようになっていくでしょう。